- トップページ
- Rによる群集組成の解析
- 多様度指数の比較
- 多様度指数の計算
多様度指数の計算
多様度指数の計算
群集組成を記述した地点×種の個体数のcsvファイルから、各地点の多様度指数(種数、Shannon多様度の指数、逆数のSimpson多様度、最優占種占有率の逆数)と地域のαβγ多様度を計算します。入力用csvファイルの形式は、2行目以降の各行が各地点のデータで最初が地点名、2番目以降が各種の個体数です。1行目は最初が地域名、2番目以降が種名ですが計算には使われないダミーです。なお、計算値の利用は利用者の責任でお願いします。
多様度指数の計算をします。参照ボタンでcsvファイルを開いてください
多様度指数とは
多様度指数は群集組成の複雑さを数値化します。ShannonのH'が有名ですが、他にも有用な指数があります。それぞれの指数は、群集組成の特徴を数値化したものですが、対象とする群集組成のどういった特徴を強調するかが異なっています。
多様度指数の系列
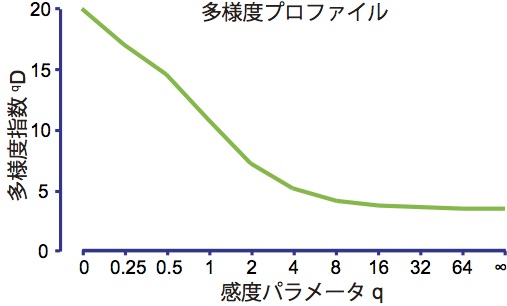
いくつかの多様度指数を統一的に理解する方策の一つとして、Renyiの多様度プロファイルというものがあります。これは、感度パラメータ(q)を変化させることによって一連の多様度指数を系列として作成するものです。種数をS、群集を構成する種を多い順に並べてi番目種の個体数が総個体数に占める割合をpi(つまりpiのなかでp1が最大)として、多様度指数qD=(Σpiq)1/(1-q)を求めます。すると、下記の有用な指数がqの系列で表現できます。
- 種数(species richness): 0D=S
- シャノン多様度の指数(exponential Shannon): 1D=exp(-Σpilog(pi))
- シンプソン多様度の逆数(inverse Simpson): 2D=1/Σpi2
- 最優占種占有率の逆数(inverse relative dominance): ∞D=1/p1
qの値を0から∞に変化させると、多様度指数qDの値が徐々に減少します。この変化を多様度プロファイルと呼びます。qは群集内の各種にかけるウェイトを変化させる作用があります。q=0だと優占種から希少種まで全ての種を同等に数え上げますが、qの増加とともに優占種のウェイトが上がり希少種のウェイトが下がり、q=∞のときには最優占種のみが指数の計算に貢献します。
これらの多様度指数は種数と同じ単位で、群集が何種分の多様性をもつかを表すため、数値の意味を理解しやすくなります。この点を強調するために有効種数と呼ばれることがあります。
多様度指数は各種の相対的な比率piをもとに計算されていますので、サンプル中の総個体数が変化しても構成種の比率が同じならば同じ値を示します。
αβγ多様度
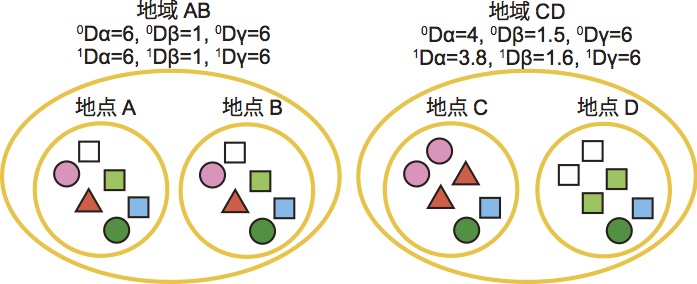
γ多様度はある地域全体の多様度、α多様度をその地域内の各地点の多様度と呼び、β多様度=γ多様度/α多様度で定義します。地点数がNあり、地点jでのi番目の種の割合をpijとします。
- α多様度: qDα=(Σ(Σpijq)/N)1/(1-q), ただし1Dα=exp(-Σ(Σpilog(pi))/N)
- β多様度: qDβ=qDγ/qDα
- γ多様度: qDγ=(Σ(Σj pij/N)q)1/(1-q), ただし1Dγ=exp(-Σ(Σj pi/N)log(Σj pi/N))
α多様度はq=0のときのみ地点全体の平均値(種数の平均値)ですが、それ以外は単純な平均値ではありません。各種の割合pijを地点全体で平均してから多様度指数を計算するとγ多様度が求められます。β多様度は地域内のユニークな群集の数を表します。
参考文献
- Magurran AE, McGill BJ (2011) Biological Diversity: Frontiers in measurement and assessment. Oxford
- 高田宜武・手塚尚明 (2016) 干潟漁場における多様度指数. 海洋と生物 227: 633-640
このページは水産庁委託「漁場環境生物多様性評価手法実証事業」の活動の一環として作成されました
高田宜武 ![]() 更新: 2018/2/16
更新: 2018/2/16
多様度指数の比較に戻る
